[Day19] 그래프

Posted Feb 20, 2025 Updated Feb 20, 2025

java

By yeeun426

20 min read

[Day19] 그래프

오늘 수업에서는 그래프에 대해 학습했습니다. BFS와 DFS는 알고리즘 풀 때 항상 어려운 부분이라 수업과 “코딩테스트 합격자 되기” 책을 참고해 정리해보았습니다.

그래프(Graph)

그래프는 노드와 간선으로 이루어진 비선형 데이터 구조

"선형 구조" ? 원소들을 하나씩 순차적으로 나열시킨 형태 
(ex) 스택, 큐

"비선형 구조" ? 하나의 자료 뒤에 여러개의 자료가 존재할 수 있는 형태
(ex) 트리, 그래프

그래프 용어 정리

정점(node): 그래프에서 하나의 점
간선(Edge): 정점 간의 연결. 부모-자식 개념 없음
가중치(Weight): 간선에 할당된 값 (거리, 비용 등)
차수(Degree): 한 정점에 연결된 간선의 수
- 진입 차수: 들어오는 간선 개수 (방향 그래프)
- 진출 차수: 나가는 간선 개수 (방향 그래프)
경로(Path): 한 정점에서 다른 정점으로 가는 간선의 연속
사이클(Cycle): 시작 정점에서 출발 → 다시 시작 정점으로 돌아오는 경로
연결 그래프: 모든 정점이 연결된 그래프
포화그래프: V 개의 정점을 가지는그래프는 최대 V * (V–1)/ 2 간선이 가능
- (ex) 4개 정점이 있는 그래프의 최대 간선수는 6 (=> 4 * 3 / 2) 개
부분 그래프: 원래 그래프의 일부 정점과 간선으로 만든 그래프

흐름을 표현하는 방향성

방향 그래프: 간선에 방향이 있음 (예: A → B)
무방향 그래프: 간선에 방향이 없음 (예: A - B)

그래프의 활용 예시

소셜 네트워크: 사람(정점)과 사람 간의 친구 관계(간선)를 나타내는 그래프.
도로망: 도로의 교차점(정점)과 도로(간선)를 표현하는 그래프.
웹 페이지: 웹 페이지(정점)와 링크(간선) 간의 관계를 나타내는 그래프

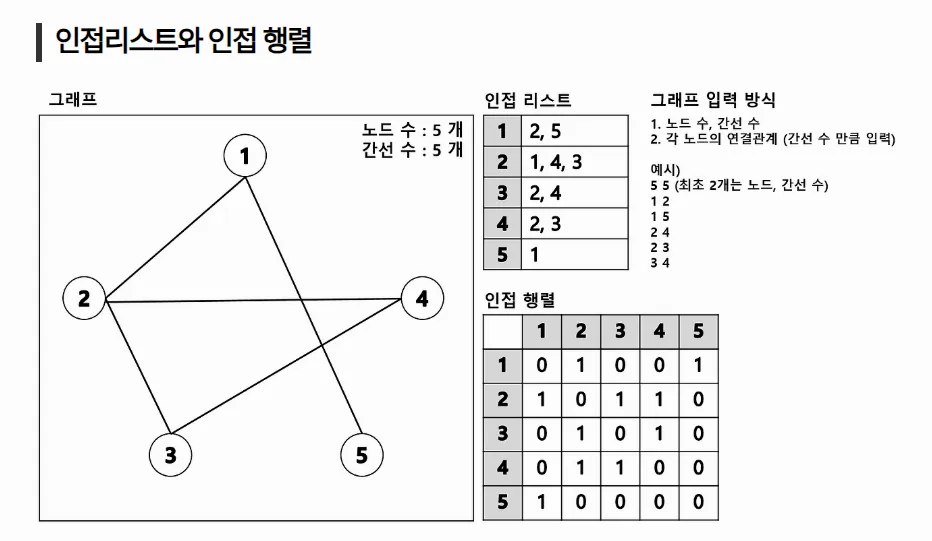
그래프를 구현 방식 (인접 행렬, 인접 리스트)

1. 인접 행렬 (Adjacency Matrix)

✅ 2차원 배열을 사용해 정점 간의 연결을 저장

장점: 특정 간선(노드 i와 j가 연결)이 있는지 확인할 때 빠름 (O(1))
단점: 정점이 많고 모든 노드에 방문해보고 싶을 때 메모리를 많이 차지함 (O(V²))

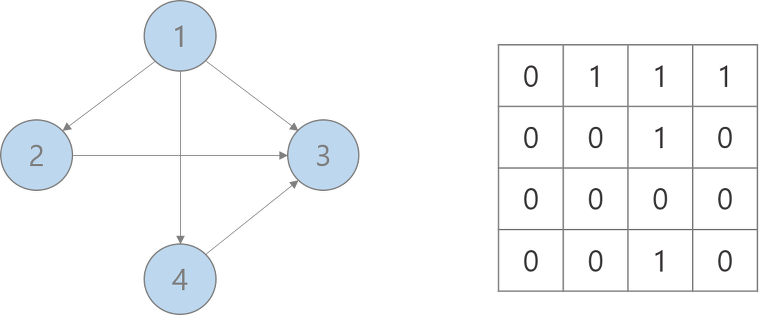
adj[i][j] : 노드 i에서 노드 j로 가는 간선이 있으면 1, 아니면 0

cf) 만약 간선에 가중치가 있는 그래프라면 1 대신에 가중치의 값을 직접 넣어주는 방식으로 구현

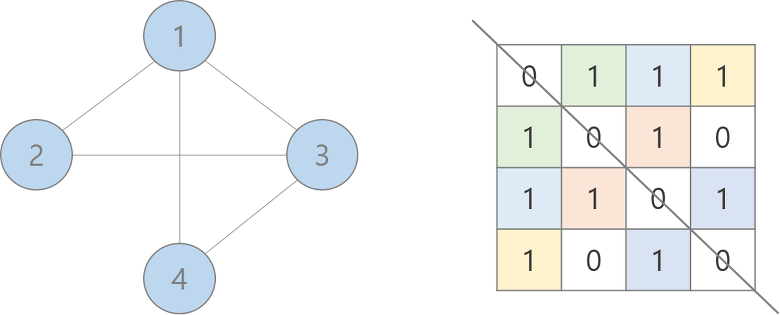
예시

방향 그래프인 경우

무방향 그래프인 경우

노드 i에서 노드 j로 가는 간선이 있다는 말은 노드 j에서 노드 i로 가는 간선도 존재한다는 의미
- 따라서, 인접 행렬이 대각 성분(adj[i][j]에서 i와 j가 같은 원소들)을 기준으로 대칭인 성질을 갖게 된다.

  
/*
첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ M ≤ N×(N-1)/2) 둘째 줄부터 M개의 줄에 간선의 양 끝점 u와 v가 주어진다. (1 ≤ u, v ≤ N, u ≠ v) 같은 간선은 한 번만 주어진다.
6 5
1 2
2 5
5 1
3 4
4 6
*/

import java.util.Scanner;

public class AdjacencyMatrix {
    public static void main(String[] args) {
        // Scanner 객체 생성하여 입력을 받을 준비
        Scanner scanner = new Scanner(System.in);
        
        // 첫 번째 줄에서 정점의 개수 N과 간선의 개수 M을 입력받음
        int N = scanner.nextInt(); // 정점의 개수
        int M = scanner.nextInt(); // 간선의 개수
        
        // N x N 크기의 인접 행렬 생성 (정점의 개수에 따라)
        int[][] adjacencyMatrix = new int[N + 1][N + 1]; // 1부터 N까지 사용하므로 N+1 크기로 생성
        
        // M개의 간선을 입력받아 인접 행렬에 저장
        for (int i = 0; i < M; i++) {
            int u = scanner.nextInt(); // 간선의 시작 정점
            int v = scanner.nextInt(); // 간선의 끝 정점
            
            // 무방향 그래프의 경우 양쪽 모두에 1을 설정
            adjacencyMatrix[u][v] = 1; // u에서 v로의 간선
            adjacencyMatrix[v][u] = 1; // v에서 u로의 간선
        }

        // 인접 행렬 출력 (디버깅 용도)
        System.out.println("인접 행렬:");
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                System.out.print(adjacencyMatrix[i][j] + " ");
            }
            System.out.println(); // 각 행을 출력한 후 줄 바꿈
        }
        // Scanner 종료
        scanner.close();
    }
}

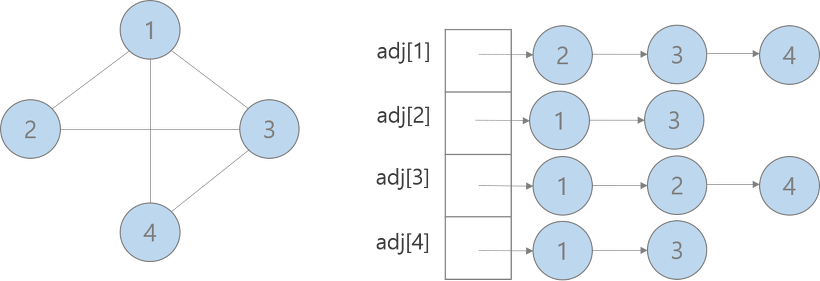
2. 인접 리스트 (Adjacency List)

✅ 배열의 각 요소가 리스트를 가짐 (정점별 연결된 정점 저장)

장점
- 간선에 비례하는 메모리만 차지
- 메모리를 절약할 수 있음 (O(V + E))
단점: 특정 간선을 찾으려면 리스트를 탐색해야 함

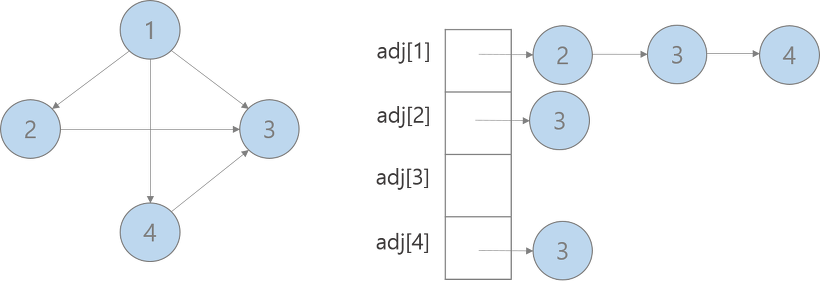
adj[i] : 노드 i에 연결된 노드들을 원소로 갖는 vector

cf) 만약 간선에 가중치가 있다면, pair<int,int> adj[]를 통해 구현 pair<int,int>의 first에는 노드의 번호, second에는 간선의 가중치를 저장하는 방식으로 저장

예시

방향 그래프인 경우

무향 그래프인 경우

  
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class AdjacencyList {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt(); // 정점 개수
        int M = scanner.nextInt(); // 간선 개수

        List<List<Integer>> adjacencyList = new ArrayList<>(N + 1);

        // 인접 리스트 초기화
        for (int i = 0; i <= N; i++) {
            adjacencyList.add(new ArrayList<>());
        }

        for (int i = 0; i < M; i++) {
            int u = scanner.nextInt();
            int v = scanner.nextInt();
            adjacencyList.get(u).add(v);
            adjacencyList.get(v).add(u);
        }

        // 인접 리스트 출력
        for (int i = 1; i <= N; i++) {
            System.out.print(i + ": ");
            for (int neighbor : adjacencyList.get(i)) {
                System.out.print(neighbor + " ");
            }
            System.out.println();
        }
        scanner.close();
    }
}

인접 행렬과 인접 리스트의 장단점

비교 항목	인접 행렬 (Adjacency Matrix)	인접 리스트 (Adjacency List)
메모리 사용량	(O(V^2)) (정점 수의 제곱)	(O(V + E)) (정점 + 간선)
간선 추가/삭제	(O(1)) (배열 접근)	(O(1)) (리스트 추가/삭제)
연결된 간선 확인	(O(1)) (배열 접근)	(O(E)) (연결된 정점 탐색)
모든 인접 노드 탐색	(O(V)) (행 전체 순회)	(O(\deg(V))) (연결된 정점만 탐색)
그래프 밀도	밀집 그래프에 적합 (간선 많을 때)	희소 그래프에 적합 (간선 적을 때)

💡 인접 리스트로 표현하면 인접 행렬보다는 메모리 효율이 좋음

그래프 탐색 (Traversal)

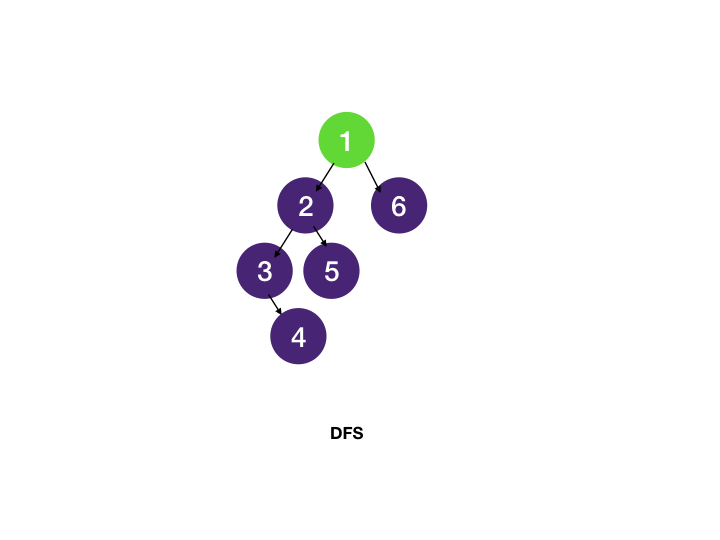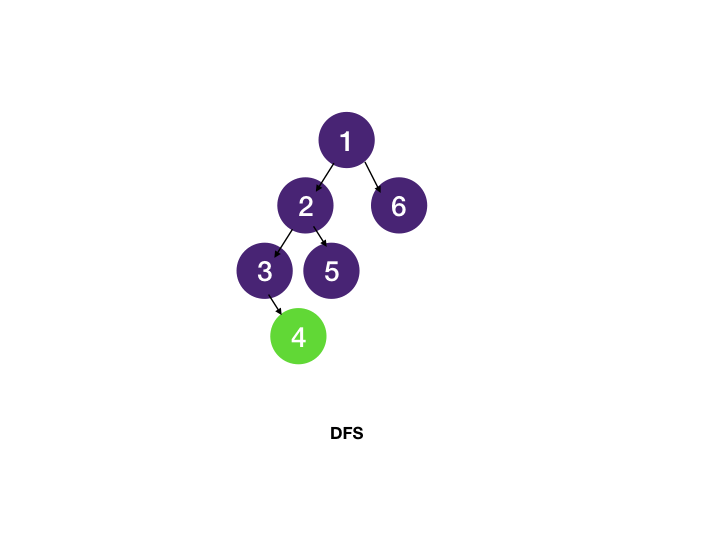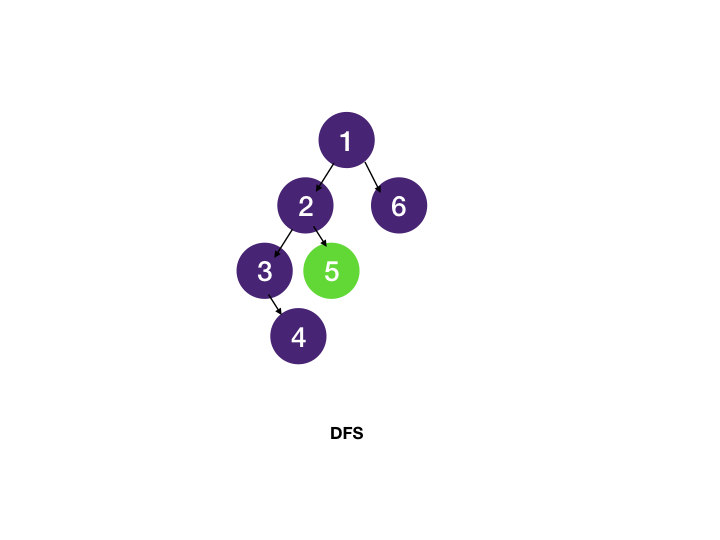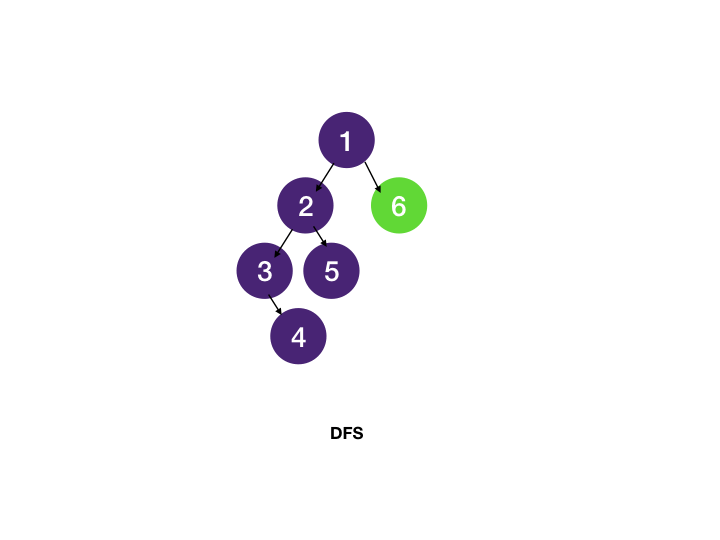
(1) DFS (Depth-First Search) - 깊이 우선 탐색

✅ 한 정점에서 출발해 한 방향으로 끝까지 탐색한 후, 다시 돌아와 다른 길 탐색

인접 행렬 구현 시 → 시간 복잡도: O(V²)
인접 리스트 구현 시 → 시간 복잡도: O(V + E)

🔹 DFS 동작 방식

시작 노드를 방문하고 출력
방문하지 않은 인접 노드를 재귀적으로 탐색

/*
정점수
간선수
탐색시작노드
간선수만큼 연결정보
*/
5
5
1
1 2
1 5
2 3
2 4
3 4

DFS - 인접 행렬 구현

  
import java.util.Scanner;

public class 백준_1260_DFS_인접행렬 {
    static int N;
    static StringBuilder sb = new StringBuilder();
    static boolean[] visited;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        N = scanner.nextInt();
        int M = scanner.nextInt();
        int start = scanner.nextInt();
        int[][] adjMatrix = new int[N + 1][N + 1];
        visited = new boolean[N + 1];

        for (int i = 0; i < M; i++) {
            int u = scanner.nextInt();
            int v = scanner.nextInt();
            adjMatrix[u][v] = adjMatrix[v][u] = 1;
        }

        dfs(adjMatrix, start);
        System.out.println(sb);
        scanner.close();
    }

    static void dfs(int[][] adjMatrix, int node) {
        visited[node] = true;
        sb.append(node).append(" ");

        for (int i = 1; i <= N; i++) {
            if (!visited[i] && adjMatrix[node][i] == 1) {
                dfs(adjMatrix, i);
            }
        }
    }
}

DFS - 인접리스트 구현

  
/*
4 5 1
1 2
1 3
1 4
2 4
3 4
*/
package temp2;

import java.util.*;

public class 백준_1260_DFS_인접리스트 {
	static List<List<Integer>> list=new ArrayList();
	static boolean[] isSelected;
	static StringBuilder sb=new StringBuilder();
	
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		
		isSelected=new boolean[n+1];
		
		for (int i = 1; i <= n+1; i++) {
			list.add(new ArrayList());
		}		
		int m=sc.nextInt();
		int startNode=sc.nextInt();
		for(int i=0;i<m;i++) {
			int u=sc.nextInt();
			int v=sc.nextInt();
			list.get(u).add(v);
			list.get(v).add(u);
		}
		dfs(startNode);
		System.out.println(sb);
	}
	
	static void dfs(int curNode) {
		isSelected[curNode]=true;
		sb.append(curNode).append(" ");
		
		for (int to : list.get(curNode)) {
			if(!isSelected[to]) {
				dfs(to);
			}
		}
	}
}

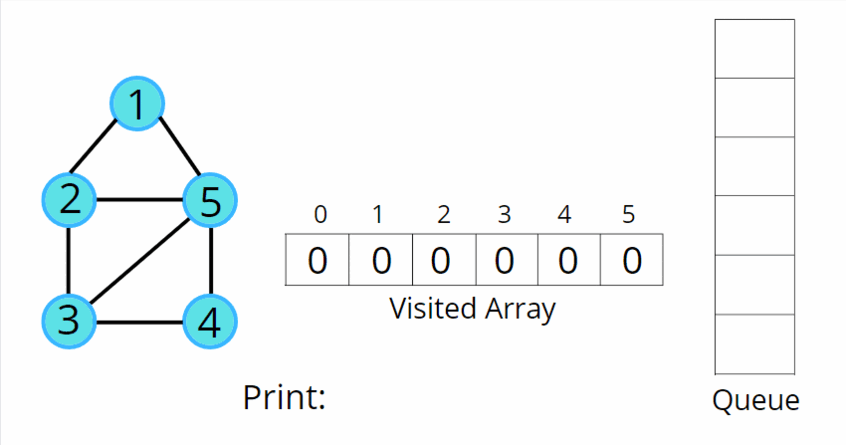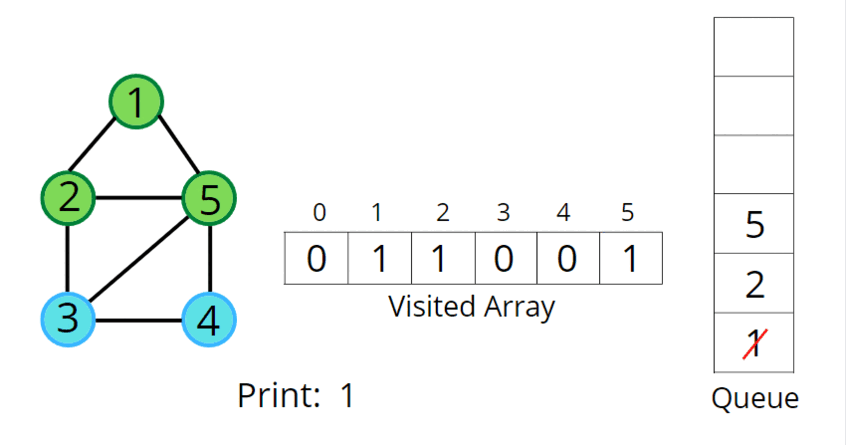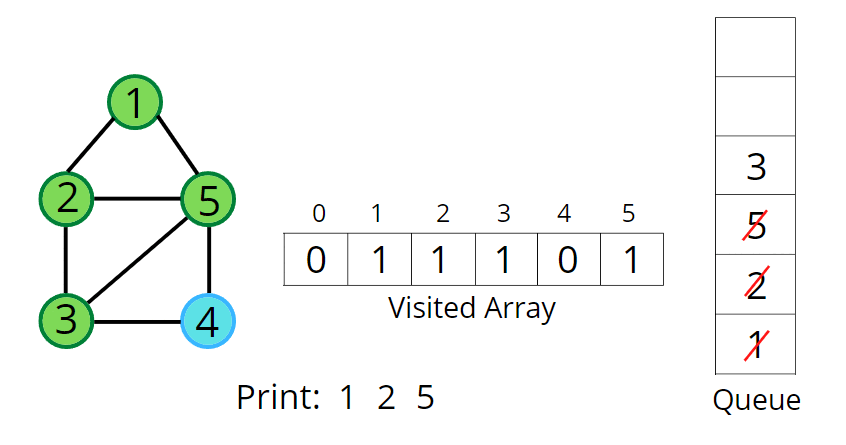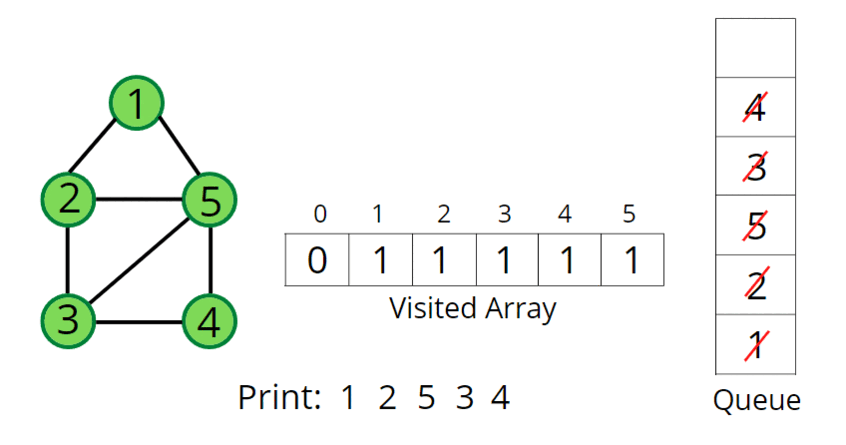
(2) BFS (Breadth-First Search) - 너비 우선 탐색

✅ 시작 정점에서 가까운 노드부터 차례로 탐색 (Queue 활용)

인접 행렬 구현 시 → 시간 복잡도: O(V²)
인접 리스트 구현 시 → 시간 복잡도: O(V + E)

🔹 BFS 동작 방식

시작 노드를 방문하고 큐에 추가
큐에서 노드를 꺼내고 인접 노드를 모두 큐에 추가

BFS - 인접 행렬 구현

  
/*
https://www.acmicpc.net/problem/1260
4 5 1
1 2
1 3
1 4
2 4
3 4
*/
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class BFS_AdjacencyMatrix {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int N = scanner.nextInt();
        int M = scanner.nextInt();
        int start = scanner.nextInt();
        int[][] adjMatrix = new int[N + 1][N + 1];
        boolean[] visited = new boolean[N + 1];

        for (int i = 0; i < M; i++) {
            int u = scanner.nextInt();
            int v = scanner.nextInt();
            adjMatrix[u][v] = adjMatrix[v][u] = 1;
        }

        Queue<Integer> queue = new LinkedList<>();
        queue.offer(start);
        visited[start] = true;

        while (!queue.isEmpty()) {
            int node = queue.poll();
            System.out.print(node + " ");

            for (int i = 1; i <= N; i++) {
                if (!visited[i] && adjMatrix[node][i] == 1) {
                    queue.offer(i);
                    visited[i] = true;
                }
            }
        }
        scanner.close();
    }
}

BFS_인접리스트 구현

  
import java.util.*;

public class 백준_1260_BFS_인접리스트 {
	static List<List<Integer>> list=new ArrayList();
	static boolean[] isSelected;
	static StringBuilder sb=new StringBuilder();
	
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		
		isSelected=new boolean[n+1];
		
		for (int i = 1; i <= n+1; i++) {
			list.add(new ArrayList());
		}		
		int m=sc.nextInt();
		int startNode=sc.nextInt();
		for(int i=0;i<m;i++) {
			int u=sc.nextInt();
			int v=sc.nextInt();
			list.get(u).add(v);
			list.get(v).add(u);
		}
		
		Queue<Integer> q=new LinkedList();
		q.offer(startNode);
		isSelected[startNode]=true;
		
		while(!q.isEmpty()) {
			int curNode=q.poll();
			sb.append(curNode).append(" ");
			
			for (int i :list.get(curNode)) {
				if(!isSelected[i]) {
					q.offer(i);
					isSelected[i]=true;
				}
			}
		}
		
		System.out.println(sb);
	}
}

수업에서 들은것만으로는 DFS, BFS 이해가 부족해서 JS를 활용한 DFS, BFS를 다시 정리해보았다.
👉🏻 DFS / BFS

GROUP STUDY

BJ 17478-재귀함수가 뭔가요?

  
import java.util.Scanner;

public class Main {
    static int n;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();

        System.out.println("어느 한 컴퓨터공학과 학생이 유명한 교수님을 찾아가 물었다.");
        print(0);
        sc.close();
    }

    static void print(int cur) {
        String prefix = "____".repeat(cur);

        if (n == cur) {
            System.out.println(prefix + "\"재귀함수가 뭔가요?\"");
            System.out.println(prefix + "\"재귀함수는 자기 자신을 호출하는 함수라네\"");
            System.out.println(prefix + "라고 답변하였지.");
            return;
        }

        System.out.println(prefix + "\"재귀함수가 뭔가요?\"");
        System.out.println(prefix + "\"잘 들어보게. 옛날옛날 한 산 꼭대기에 이세상 모든 지식을 통달한 선인이 있었어.");
        System.out.println(prefix + "마을 사람들은 모두 그 선인에게 수많은 질문을 했고, 모두 지혜롭게 대답해 주었지.");
        System.out.println(prefix + "그의 답은 대부분 옳았다고 하네. 그런데 어느 날, 그 선인에게 한 선비가 찾아와서 물었어.\"");

        print(cur + 1);

        System.out.println(prefix + "라고 답변하였지.");
    }
}

1954-D2 달팽이숫자

  
import java.util.Scanner;

public class Solution {
    static StringBuilder sb = new StringBuilder();

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int T = sc.nextInt();

        for (int i = 0; i < T; i++) {
            int N = sc.nextInt();
            
            // 우, 하, 좌, 상 방향 이동 배열
            int[] dx = {0, 1, 0, -1}; 
            int[] dy = {1, 0, -1, 0}; 

            int[][] arr = new int[N][N];
            sb.append("#").append(i + 1).append("\n");

            int x = 0, y = 0, dir = 0; // 초기 위치 및 방향 설정

            for (int j = 1; j <= N * N; j++) {
                arr[x][y] = j; // 현재 위치에 숫자 삽입
                
                int nx = x + dx[dir]; 
                int ny = y + dy[dir]; 

                // 범위를 벗어나거나 이미 값이 채워진 경우 방향 전환
                if (nx < 0 || nx >= N || ny < 0 || ny >= N || arr[nx][ny] != 0) {
                    dir = (dir + 1) % 4;
                    nx = x + dx[dir];
                    ny = y + dy[dir];
                }
                x = nx; // x 갱신
                y = ny; // y 갱신
            }
            // 배열 출력
            for (int s = 0; s < N; s++) {
                for (int t = 0; t < N; t++) {
                    sb.append(arr[s][t]).append(" ");
                }
                sb.append("\n");
            }
        }
        System.out.println(sb);
        sc.close();
    }
}

이 문제는 다같이 풀고 혼자 이해가 안되는 부분이 있어서 다른 팀원분이 설명해주셨다 ! 그 설명을 토대로 그림 그리면서 이해한 것을 따로 포스팅 해보았습니다 !

👉🏻 1954-D2 달팽이숫자 풀이 포스팅

1873-D3 상호의 배틀필드

이 문제는 이해하기도, 코드도 너무 까다로워서 다른 사람이 푼 풀이를 보면서 한줄씩 이해해보았습니다..

참고한 블로그 :

1873-D3 상호의 배틀필드

Reference

이 포스트는 아래 게시글의 정보 및 이미지가 사용되었습니다.

[그래프] 인접 행렬과 인접 리스트
참고 도서 “코딩테스트 합격자 되기 자바편”

END

Ureca, Algorithm

This post is licensed under CC BY 4.0 by the author.

그래프(Graph)

그래프 용어 정리

흐름을 표현하는 방향성

그래프의 활용 예시

그래프를 구현 방식 (인접 행렬, 인접 리스트)

1. 인접 행렬 (Adjacency Matrix)

예시

2. 인접 리스트 (Adjacency List)

예시

인접 행렬과 인접 리스트의 장단점

그래프 탐색 (Traversal)

(1) DFS (Depth-First Search) - 깊이 우선 탐색

🔹 DFS 동작 방식

DFS - 인접 행렬 구현

DFS - 인접리스트 구현

(2) BFS (Breadth-First Search) - 너비 우선 탐색

🔹 BFS 동작 방식

BFS - 인접 행렬 구현

BFS_인접리스트 구현

GROUP STUDY

BJ 17478-재귀함수가 뭔가요?

1954-D2 달팽이숫자

1873-D3 상호의 배틀필드

Reference

END

Trending Tags