[Day18] 비선형 자료구조

Posted Feb 19, 2025

java

By yeeun426

11 min read

[Day18] 비선형 자료구조

비선형 자료구조

데이터가 선형(순차적)으로 배치되지 않고, 계층적 또는 복잡한 관계를 갖는 구조
필요성 : 복잡한 관계를 표현하고 효율적인 데이터 검색 및 관리 가능

종류

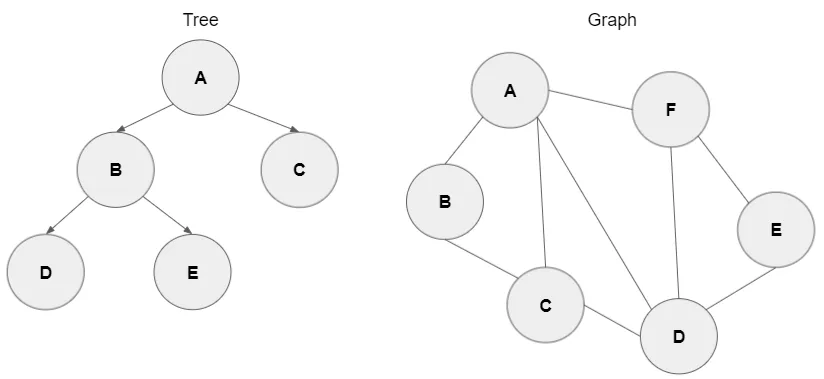
트리(Tree)
그래프(Graph)

트리(Tree)

기본 용어 ⭐️⭐️⭐️

노드(Node) : 데이터의 단위(정점)
루트(Root) : 트리의 최상위 노드
리프(Leaf) : 자식이 없는 노드
서브트리(Subtree) : 특정 노드를 루트로 하는 하위 트리
높이(Height) : 루트에서 가장 깊은 리프까지의 경로 길이
깊이(Depth) : 특정 노드가 루트에서 얼마나 떨어져 있는지
간선(Edge) : 부모 노드와 자식 노드를 연결하는 선
- 트리는 사이클이 없고, 연결되어 있어야 함
- 노드 수가 n이면 간선의 수는 n-1

트리 활용 예시

파일 시스템 : 컴퓨터의 파일 시스템
- 정점 : 폴더와 파일 구조
- 간선 : 폴더가 포함하는 파일이나 하위 폴더 간의 관계
- 설명 : 최상위 폴더(루트)가 있고, 그 아래에 여러 하위 폴더가 있으며, 각 하위 폴더는 또 다른 파일이나 폴더를 포함할 수 있음
조직도 : 회사의 계층 구조
- 정점: 직원
- 간선: 상사와 부하 직원 간의 관계
- 설명: CEO가 루트 노드가 되고, 각 부서의 관리자와 그 아래의 직원들이 자식 노드로 연결됨
가족 트리 : 가계도
- 정점: 가족 구성원 (부모, 자식, 조부모 등)
- 간선: 부모와 자식 간의 관계
- 설명: 한 사람을 루트로 하고, 그 사람의 부모, 자식, 조부모 등을 나열하여 가족 관계를 시각화
우선순위 큐(Heap) : 힙 구조
- 정점: 요소
- 간선: 부모 노드와 자식 노드 간의 관계
- 설명: 최소 힙 또는 최대 힙 구조에서 각 요소는 부모 노드와 자식 노드로 연결되어 우선 순위를 유지

이진 트리 순회 (Tree Traversal)

트리를 탐색하는 방법에는 3가지가 있음

🔹 전위 순회 (Pre-order) 🔹

순서: (루트) → (왼쪽) → (오른쪽)

  
static void preOrder(char node) {
 if (node == '.') return;
 System.out.print(node);
 if (tree.containsKey(node)) {
   Character[] children = tree.get(node);
   if (children[0] != null) preOrder(children[0]);
   if (children[1] != null) preOrder(children[1]);
 }
}

🔹 중위 순회 (In-order) 🔹

순서: (왼쪽) → (루트) → (오른쪽)

  
static void inOrder(char node) {
 if (node == '.') return;
 if (tree.containsKey(node)) {
   Character[] children = tree.get(node);
   if (children[0] != null) inOrder(children[0]);
 }
 System.out.print(node);
 if (tree.containsKey(node)) {
   Character[] children = tree.get(node);
   if (children[1] != null) inOrder(children[1]);
 }
}

🔹 후위 순회 (Post-order) 🔹

순서: (왼쪽) → (오른쪽) → (루트)

  
static void postOrder(char node) {
 if (node == '.') return;
 if (tree.containsKey(node)) {
   Character[] children = tree.get(node);
   if (children[0] != null) postOrder(children[0]);
   if (children[1] != null) postOrder(children[1]);
 }
 System.out.print(node);
}

이진 검색(Binary Search)

어떤 노드를 찾기 위해 모든 노드를 순회해야 한다면(완전탐색) O(n)이 된다. 이것을 O(log n)으로 만들 수 있는 방법이 이진 검색이다.

이진 검색의 조건

데이터가 정렬되어 있어야 함

📌 1차원 배열에서 이진 검색 예제

  
public class BinarySearch {
    public static int binarySearch(int[] arr, int target) {
        int low = 0, high = arr.length - 1;
        while (low <= high) {
            int mid = (low + high) / 2;
            if (arr[mid] == target) return mid;
            else if (arr[mid] < target) low = mid + 1;
            else high = mid - 1;
        }
        return -1;
    }
}

트리구조에서 이진검색되는 API : java.util.TreeSet

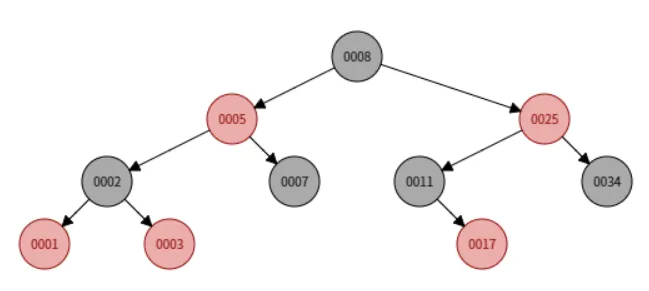
편향 트리가 되면 O(log n)을 유지할 수 없고  O(n)이 되버리기 때문에 균형을 맞추기 위한 Red-Black Tree 라는 알고리즘으로 구현되어 있다

❗️ 규칙 ❗️
1. 삽입된 노드의 부모가 RED이며 삼촌 노드도 RED인 경우
조치: 부모와 삼촌을 BLACK으로 바꾸고 조부모를 RED로 바꿉니다. (칼라 반전만으로 해결)
2. 삽입된 노드가 부모의 오른쪽 자식이고, 부모가 할아버지의 왼쪽 자식이며, 삼촌이 BLACK인 경우
조치: 부모를 기준으로 왼쪽으로 회전한 후, 삽입된 노드와 부모의 색상을 조정합니다.
3. 삽입된 노드가 부모의 왼쪽 자식이고, 부모가 할아버지의 왼쪽 자식이며, 삼촌이 BLACK인 경우
조치: 부모와 할아버지의 색을 바꾼 후, 할아버지를 기준으로 오른쪽으로 회전합니다.
4. 삽입된 노드가 부모의 오른쪽 자식이고, 부모가 할아버지의 오른쪽 자식이며, 삼촌이 BLACK인 경우
조치: 부모와 할아버지의 색을 바꾼 후, 할아버지를 기준으로 왼쪽으로 회전합니다.
5. 삽입된 노드가 부모의 왼쪽 자식이고, 부모가 할아버지의 오른쪽 자식이며, 삼촌이 BLACK인 경우
조치: 부모를 기준으로 오른쪽으로 회전한 후, 삽입된 노드와 부모의 색상을 조정합니다.

✅ 중위 순회
1 -> 2 -> 3 -> 5 -> 7 -> 8 -> 11 -> 17 -> 25 -> 34

📌 TreeSet 예제

  
import java.util.TreeSet;

public class TreeSetExample {
    public static void main(String[] args) {
        // TreeSet 생성
        TreeSet<Integer> treeSet = new TreeSet<>();

        treeSet.add(5);   // 5 추가
        treeSet.add(3);   // 3 추가
        treeSet.add(8);   // 8 추가
        treeSet.add(1);   // 1 추가
        treeSet.add(7);   // 7 추가
        treeSet.add(25);
        treeSet.add(34);
        treeSet.add(2);
        treeSet.add(11);
        treeSet.add(17);

        // 요소 출력 (자동으로 정렬됨)
        System.out.println("TreeSet의 요소: " + treeSet); // [1, 2, 3, 5, 7, 8, 11, 17, 25, 34]

        // 특정 요소 검색
        int searchElement = 5;
        if (treeSet.contains(searchElement)) {
            System.out.println("5는 존재");
        } else {
            System.out.println("5는 존재하지 않음");
        }

        // 최소값과 최대값 찾기
        int minElement = treeSet.first(); // 최소값
        int maxElement = treeSet.last();  // 최대값
        System.out.println("최소값: " + minElement); // 출력: 1
        System.out.println("최대값: " + maxElement); // 출력: 8

        // 요소 삭제
        treeSet.remove(3); // 3 삭제
        System.out.println("3을 삭제한 후 TreeSet의 요소: " + treeSet); // 출력: [1, 5, 7, 8]

        // 부분 집합 (서브셋) 생성 -> 캐스팅 해줘야함.
        TreeSet<Integer> subSet = (TreeSet<Integer>) treeSet.subSet(5, true, 8, true);
        System.out.println(subSet); // 출력: [5, 7, 8]
    }
}

TreeSet vs HashSet

비교 항목	TreeSet	HashSet
내부 구조	이진 탐색 트리	해시 테이블
정렬 여부	자동 정렬 O	정렬 X, 순서 보장 X
탐색 속도	O(log n)	O(1)
삽입/삭제	O(log n)	O(1)

✅ set에서 정렬할 일이 많이 없어서 굳이 treeSet보다는 HashSet을 사용함 (훨씬 빠르니깐 !)

📌 TreeSet vs HashSet 성능 비교

  
import java.util.*;

public class SetPerformanceComparison {
    public static void main(String[] args) {
        int n = 100000;

        // TreeSet 성능 테스트
        long startTime = System.nanoTime();
        TreeSet<Integer> treeSet = new TreeSet<>();
        for (int i = 0; i < n; i++) treeSet.add((int) (Math.random() * n));
        long endTime = System.nanoTime();
        System.out.println("TreeSet 삽입 시간: " + (endTime - startTime) + " ns"); 

        // HashSet 성능 테스트
        startTime = System.nanoTime();
        HashSet<Integer> hashSet = new HashSet<>();
        for (int i = 0; i < n; i++) hashSet.add((int) (Math.random() * n));
        List<Integer> hashList = new ArrayList<>(hashSet);
        Collections.sort(hashList);
        endTime = System.nanoTime();
        System.out.println("HashSet 삽입 및 정렬 시간: " + (endTime - startTime) + " ns");
    }
}

-> HashSet에서 ArrayList로 정렬하더라도 treeSet보다 더 빠르고 성능이 좋다 !

❓ 빅오 -> 최악의 수행 시간

👉🏻팀플 알고리즘

END

Ureca, Algorithm

This post is licensed under CC BY 4.0 by the author.