[Day17] 순열 / 조합 / 부분집합

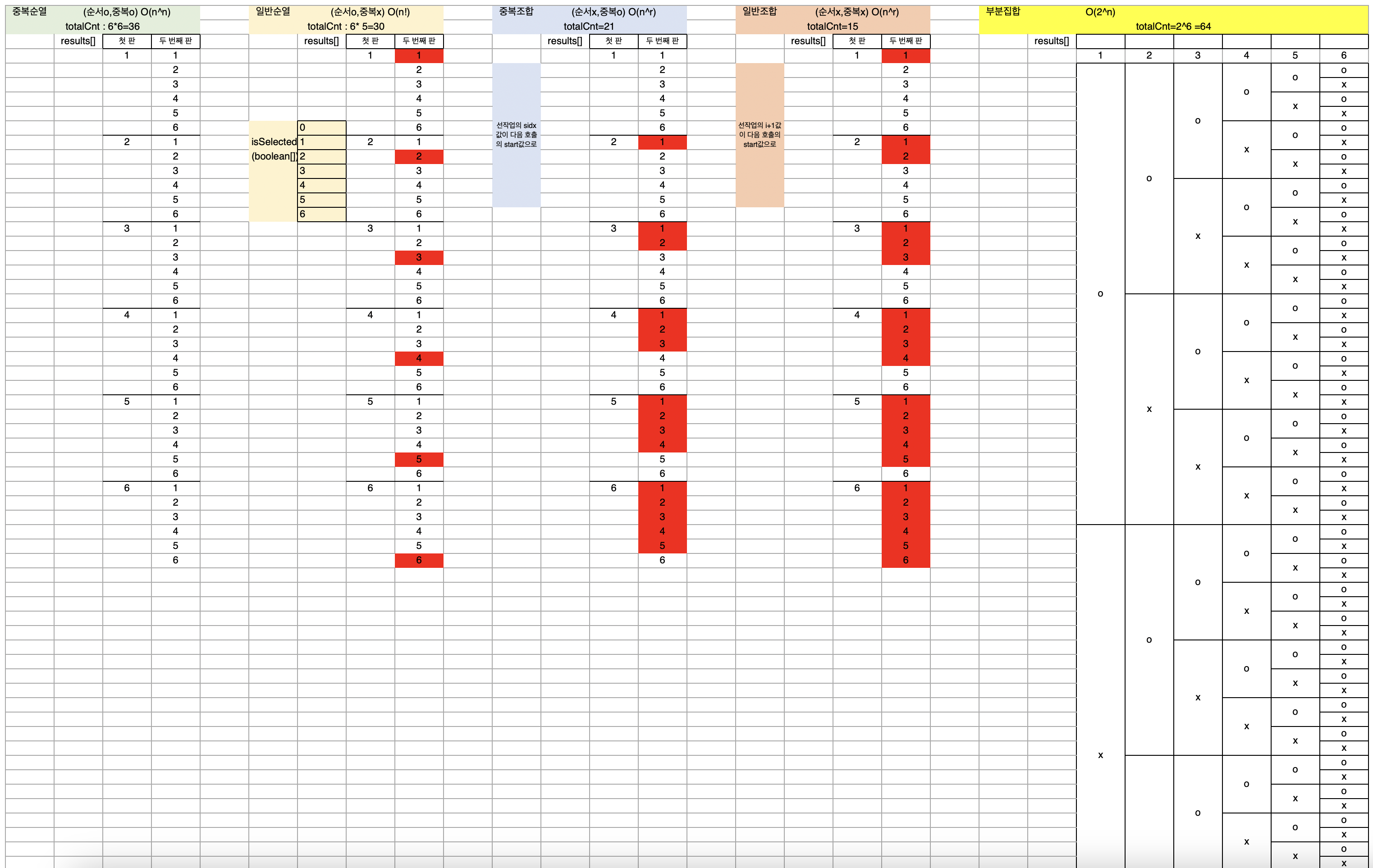
순열 (Permutation)

• 순서가 중요하며 중복을 허용하지 않음
• 가능한 모든 경우를 고려해야 하므로 시간복잡도는 O(n!)

(ex) 주사위 던지기 (순열)

import java.util.Arrays;

public class A01_주사위_일반순열 {
    static int totalCnt; // 완성된 순열의 수
    static int n; // 주사위 던지는 횟수
    static int[] results; // 순열 결과를 저장할 배열
    static boolean[] isSelected; // 중복 체크를 위한 배열

    public static void main(String[] args) {
        n = 2; // 주사위를 2번 던짐
        results = new int[n];
        isSelected = new boolean[7]; // 1~6번 index만 사용
        주사위던지기(0);
        System.out.println(totalCnt);
    }


	//주사위-일반순열(순서 o, 중복 x)
	public static void 주사위던지기(int cnt) {//cnt는 판의 횟수
		//ex. 주사위를 2번 던져서 나오는 모든 경우의 수, 한번 뽑은 걸 다시 뽑을 수 없음==> 중복 체크 코드 있음 : 30
		if(cnt==n) {// cnt는 판의 횟수
			totalCnt++;
			System.out.println(Arrays.toString(results));
			return;
		}

        for (int i = 1; i <= 6; i++) {
            if (isSelected[i]) continue;
            results[cnt] = i;
            isSelected[i] = true;
            주사위던지기(cnt + 1);
            isSelected[i] = false;
        }
    }
}

📌 Explanation

• isSelected 배열을 사용하여 중복을 방지
• cnt == n일 때 결과 출력
• for문에서 사용한 숫자는 다시 사용하지 않도록 isSelected[i] = true

훈련문제 - 모든 순열 (https://www.acmicpc.net/problem/10974)

package 순조부;

import java.util.Scanner;
public class 백준10974_모든순열 {
	static int n;
	static int[] result;
	static boolean[] isSelected;
	static StringBuilder sb = new StringBuilder();
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt();
		result = new int[n];
		isSelected = new boolean[n+1];	
		perm(0);
		System.out.println(sb);
	}
	
	private static void perm(int cnt) {
		if(cnt == n) {
			for(int i : result) {
				sb.append(i).append(" ");
			}
			sb.append("\n");
			return;
		}
		for(int i = 1 ; i <= n ; i++) {
			if(isSelected[i]) continue;
			result[cnt] = i;
			isSelected[i] = true;
			perm(cnt + 1);
			isSelected[i] = false;
		}
	}
}

---

조합 (Combination)

• 순서는 중요하지 않으며, 중복을 허용하지 않음
• 일반적으로 재귀를 이용하여 해결
• 시간복잡도: O(2^n) ~ O(nCr)

(ex) 주사위 던지기 (조합)

import java.util.Arrays;

public class A02_주사위_일반조합 {
	static int totalCnt; // 완성된 조합의 수
	static int n;// 주사위 던지는 횟수
	static int[] results;// 조합 결과를 저장할 배열
	
	public static void main(String[] args) {
		n = 2; // 2회
		results = new int[n];
		//첫 번째 인수는 판 번호로 0부터 시작해야 배열에 집어 넣기 좋다.
		주사위던지기(0, 1);//두 번째 인수는 순서와 중복을 없애기 위한 아이디어.최초에는 주사위의 가장 작은 숫자 1부터 부여.
		System.out.println(totalCnt);
	}

	// 주사위-일반조합
	public static void 주사위던지기(int cnt, int start) {// 일반조합(순서 x,중복 x) 
		if (cnt == n) {
			totalCnt++; //최종 15
			System.out.println(Arrays.toString(results));
			return;
		}
		for (int i = start; i <= 6; i++) {
			results[cnt] = i;
			주사위던지기(cnt + 1, i + 1); //두 번째 판을 던지러 갈 때 지금의 i 값보다 1큰수로 시작하게 하면 중복과 순서를 모두 피할 수 있다
		}
	}
}

📌 Explanation

• start 값을 사용하여 중복을 방지
• 주사위던지기(cnt + 1, i + 1); → 이전 값보다 큰 숫자만 선택

---

부분집합 (Subset)

• 모든 경우의 조합을 고려해야 하며, 선택하거나 선택하지 않는 2가지 경우로 진행
• 시간복잡도: O(2^n)

(ex) 주사위 숫자의 부분집합

package test;

public class A03_주사위_부분집합 {	
	static int totalCnt; // 부분집합의 총 개수를 저장하는 변수	
	static int[] input={1, 2, 3, 4, 5, 6};// 주사위의 숫자를 가진 배열	
	static boolean[] isSelected;// 각 숫자가 선택되었는지를 저장하는 배열
	
	public static void main(String[] args) {		
		
		isSelected = new boolean[6];	// 선택 여부를 저장할 배열 초기화		
		subset(0);// 부분집합 생성 함수 호출		
		
		System.out.println(totalCnt);// 생성된 부분집합의 총 개수 출력
	}
	
	// 부분집합 생성 함수
	public static void subset(int cnt) {
		// cnt가 6이면 모든 원소를 고려한 상태이므로 부분집합을 하나 완성한 것
		if (cnt == 6) {
			// 완성된 하나의 부분집합 개수 증가
			++totalCnt;
			// 현재 완성된 부분집합 출력
			for (int i = 0; i < 6; i++) {
				// 선택된 원소는 출력하고, 선택되지 않은 원소는 "X"로 표시
				System.out.print((isSelected[i] ? input[i] : "X") + " ");
			}
			System.out.println(); 
			return; 
		}
		
		// 현재 원소를 선택하는 경우
		isSelected[cnt] = true; // 선택 상태로 설정
		subset(cnt + 1); // 다음 원소로 진행
		
		// 현재 원소를 비선택하는 경우
		isSelected[cnt] = false; // 비선택 상태로 설정
		subset(cnt + 1); // 다음 원소로 진행
	}
}

📌 Explanation

• isSelected[cnt] = true → 현재 원소 포함
• isSelected[cnt] = false → 현재 원소 미포함
• 모든 경우를 탐색

✅ 정리

구분	중복	순서	시간복잡도
순열	X	O	O(n!)
조합	X	X	O(nCr)
부분집합	-	X	O(2^n)

🔹 언제 사용할까?

• 순열: 모든 경우의 수를 고려할 때 (ex. 암호 생성, 경로 탐색)
• 조합: 선택된 원소들만 고려할 때 (ex. 팀 구성, 메뉴 조합)
• 부분집합: 특정 조건을 만족하는 부분 집합을 찾을 때 (ex. 특정 합을 만드는 집합)

---

👉🏻내가 만든 예제

---

👉🏻팀플 알고리즘