[Day22] 백트래킹 & 위상정렬
[Day22] 백트래킹 & 위상정렬
백트래킹 (Backtracking)
해를 찾기 위해서 후보군을 나열하고, 만약 조건에 맞지 않다면 후보군에서 제외하고 돌아와 다음 후보군을 찾는 방식
- 트리 구조에서 DFS(깊이 우선 탐색) 기반으로 진행
- Promising (부합한지 체크): 현재 경로가 조건을 만족하는지 확인
- Pruning (가지치기): 조건을 만족하지 않으면 더 깊이 탐색하지 않고 중단
- 상태 공간 트리(State Space Tree)를 활용하여 검색할 후보를 관리
N-Queens 문제 예제
N-Queens 문제는 N×N 체스판에서 N개의 퀸이 서로 공격하지 않도록 배치하는 문제
시간복잡도 O(n!)
8-Queens라면 8^8=16,000,000이 넘는 경우의 수를 확인해야 하는데 Pruning을 하면 약 4000~5000정도만 탐색하여 92개의 해를 얻게 됨.
4-Queens 코드 분석
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import java.util.LinkedList;
import java.util.List;
public class Jes_NQueens {
static int N = 4; // 4x4 체스판
static List<Position> promise = new LinkedList<>();
static int promiseSetCnt;
public static void main(String[] args) {
dfs(0); // 첫 번째 행부터 시작
System.out.println("result: " + promiseSetCnt);
}
static void dfs(int curRow) {
System.out.println("현재 행: " + curRow); // 현재 행 출력
if (curRow == N) { // N번만큼 돌았다면
promiseSetCnt++; // 완성된 세트를 카운트
System.out.println("=====>완성된 세트: " + promise); // 완성된 세트 출력
return;
}
for (int col = 0; col < N; col++) {
if (isSafe(curRow, col)) { // 이 위치가 유망하면
promise.add(new Position(curRow, col)); // 현재 위치를 유망목록에 넣는다
System.out.println("퀸 추가: " + promise); // 현재 유망 목록 출력
dfs(curRow + 1); // 다음 행으로 이동
promise.remove(promise.size() - 1); // 마지막으로 추가한 퀸을 제거
System.out.println("퀸 제거: " + promise); // 유망 목록에서 퀸 제거 후 출력
} else { //백트래킹
System.out.println("위치 안전하지 않음: (" + curRow + ", " + col + ")"); // 안전하지 않은 위치 출력
}
}
}
// 현재 위치에 퀸을 배치할 수 있는지 확인하는 메소드
static boolean isSafe(int curRow, int col) {
for (Position queen : promise) {
// 유망목록에 들어가 있는 퀸들과 열이 같으면 탈락
if (col == queen.col) return false;
// 유망목록에 들어가 있는 퀸들의 대각선(X2 - X1 = |Y1-Y2| )에 있으면 탈락
if (curRow - queen.row == Math.abs(col - queen.col)) return false;
}
return true; // 유망 위치
}
static class Position {
int row, col;
Position(int row, int col) {
this.row = row;
this.col = col;
}
@Override
public String toString() {
return "Position [" + row + "," + col + "]";
}
}
}
햄버거 다이어트에서 백트래킹
맛의 합이 가장 크면서 칼로리 제한을 넘지 않는 조합을 찾는 문제
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import java.util.Scanner;
public class SWEA5215_햄버거다이어트_DFS {
static int N, L;
static int[] tastes, cals;
static boolean[] isSelected;
static int result;
static StringBuilder sb=new StringBuilder();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
long start=System.nanoTime();
for (int tc = 1; tc <= T; tc++) {
N = sc.nextInt();// 재료의 수
L = sc.nextInt();// 기준 총 칼로리
tastes = new int[N];
cals = new int[N];
isSelected = new boolean[N];
for (int i = 0; i < N; i++) {
tastes[i] = sc.nextInt();// 각 재료의 맛
cals[i] = sc.nextInt();// 각 재료의 칼로리
}
// 입력 끝
// 처리 시작
result=0;//맛의 합중 가장 큰 수
subset(0,0,0);
sb.append("#").append(tc).append(" ").append(result).append("\n");
}
System.out.println(sb);
long end=System.nanoTime();
System.out.println(end-start);
}
private static void subset(int cnt, int tastesSum, int calsSum) {
if(calsSum>L) {//칼로리 합이 기준 칼로리를 넘어버리면 이 결과 집합 세트는 버림
return;
}
//두 if 절의 순서가 중요함. 기준 칼로리를 넘어 버리면 result값을 갱신하지 않고 바로 리턴해버려야 하므로.
if(cnt==N) {
//int tastesSum=0,calsSum=0;
// for(int i=0;i<N;i++) {
// if(isSelected[i]) {//이 자리의 재료가 선택되어 있으면
// tastesSum+=tastes[i];//맛 더하기
// calsSum+=cals[i];//칼로리 더하기
// if(calsSum>L) {//칼로리 합이 기준 칼로리를 넘어버리면 이 결과 집합 세트는 버림
// return;
// }
// }
// }
result=Math.max(tastesSum, result);//더 큰 맛으로 갱신
return;
}
//isSelected[cnt]=true;
subset(cnt+1, tastesSum+tastes[cnt], calsSum+cals[cnt]);
//isSelected[cnt]=false;
subset(cnt+1, tastesSum, calsSum);
}
}
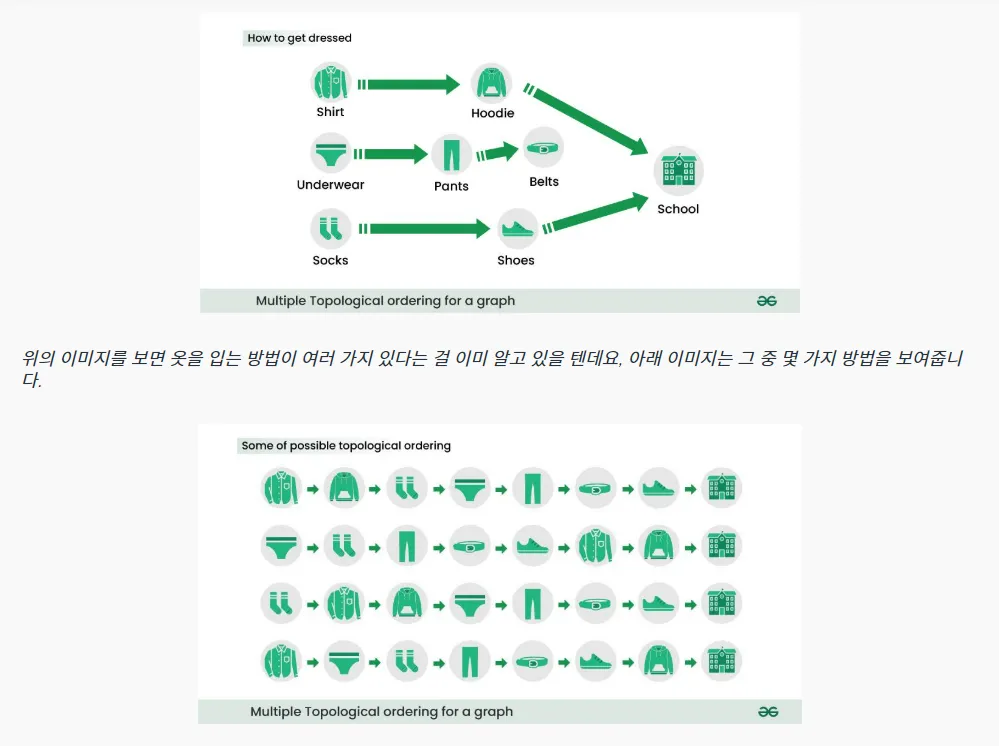
위상 정렬 (Topological Sorting)
위상 정렬은 방향 그래프의 정점들을 선형으로 배열하는 방법으로, 주로 의존성 문제에서 사용. 사이클이 없을 때만 가능
방법
- 진입 차수 계산: 각 정점의 진입 차수(해당 정점으로 들어오는 간선의 수)를 계산합니다.
- 큐에 추가: 진입 차수가 0인 정점을 큐에 추가합니다.
- 정점 처리: 큐에서 정점을 하나씩 꺼내어 결과 리스트에 추가하고, 그 정점과 연결된 모든 정점의 진입 차수를 감소시킵니다. 만약 진입 차수가 0이 되는 정점이 있다면 큐에 추가합니다.
- 결과 확인: 모든 정점을 처리했는지 확인합니다. 처리된 정점의 수가 원래 정점의 수와 같다면 위상 정렬이 성공한 것
개념 정리
- 진입 차수(In-degree) 개념 활용:
→ 어떤 정점으로 들어오는 간선의 개수를 의미 - 진입 차수가 0인 노드부터 처리
- 진입 차수가 0이 되는 노드를 큐에 추가하며 반복
- 사이클이 없는 DAG(Directed Acyclic Graph, 방향 비순환 그래프)에서만 가능
백준_1766번_문제집
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
/*
https://www.acmicpc.net/problem/1766
입력
4 2
4 2
3 1
출력
3 1 4 2
조건
1.N개의 문제는 모두 풀어야 한다.
2.먼저 푸는 것이 좋은 문제가 있는 문제는, 먼저 푸는 것이 좋은 문제를 반드시 먼저 풀어야 한다.
3.가능하면 쉬운 문제부터 풀어야 한다.
*/
import java.util.*;
public class 위상정렬 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 문제 수(N)와 의존 관계 수(M) 입력
int N = sc.nextInt();
int M = sc.nextInt();
// 그래프를 위한 인접 리스트 초기화
List<List<Integer>> graph = new ArrayList<>(N + 1);
for (int i = 0; i <= N; i++) {
graph.add(new ArrayList<>()); // 각 정점에 대해 빈 리스트 추가
}
// 진입 차수 배열 초기화
int[] inDegree = new int[N + 1];
// 의존 관계 입력 처리
for (int i = 0; i < M; i++) {
int a = sc.nextInt(); // 선행 문제
int b = sc.nextInt(); // 후행 문제
graph.get(a).add(b); // 그래프에 간선 추가
inDegree[b]++; // 후행 문제의 진입 차수 증가
}
// 위상 정렬을 위한 최소 힙(우선순위 큐) 초기화
//Queue<Integer> pq = new LinkedList<>();
//3번 조건때문에 pq로 해야 함
PriorityQueue<Integer> pq = new PriorityQueue<>();
// 진입 차수가 0인 문제들을 큐에 추가
for (int i = 1; i <= N; i++) {
if (inDegree[i] == 0) {
pq.offer(i);
}
}
// 위상 정렬 결과를 저장할 리스트
List<Integer> result = new ArrayList<>();
// 큐가 비어있지 않을 때까지 반복
while (!pq.isEmpty()) {
int current = pq.poll(); // 큐에서 문제 하나 꺼내기
result.add(current); // 현재 문제를 결과 리스트에 추가
// 현재 문제에 의존하는 문제들에 대해
for (int neighbor : graph.get(current)) {
inDegree[neighbor]--; // 진입 차수 감소
if (inDegree[neighbor] == 0) { // 진입 차수가 0이 되면
pq.offer(neighbor); // 큐에 추가
}
}
}
// 결과 출력
for (int problem : result) {
System.out.print(problem + " "); // 문제 번호 출력
}
sc.close(); // 스캐너 닫기
}
}
TEAM STUDY
백준_2252_줄 세우기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import java.util.*
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
List<List<Integer>> graph = new ArrayList<>();
for(int i = 0; i <= N; i++) {
graph.add(new ArrayList<>());
}
int[] inDegree = new int[N+1];
for(int i = 0; i < M; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph.get(a).add(b);
inDegree[b]++;
}
Queue<Integer> q = new LinkedList<>();
for(int i = 1; i <= N; i++) {
if(inDegree[i] == 0) {
q.offer(i);
}
}
List<Integer> result = new ArrayList<>();
while(!q.isEmpty()) {
int current = q.poll();
result.add(current);
for(int n:graph.get(current)) {
inDegree[n]--;
if(inDegree[n] == 0) {
q.offer(n);
}
}
}
for(int r: result) {
System.out.print(r + " ");
}
sc.close();
}
}
SWEA_1251_하나로
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
import java.util.PriorityQueue;
import java.util.Scanner;
public class Solution {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringBuilder sb = new StringBuilder();
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int N = sc.nextInt();
int[][] arr = new int[N][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < N; j++) {
arr[j][i] = sc.nextInt();
}
}
double E = sc.nextDouble(); // 환경 부담 세율
double[][] arr2 = new double[N][N];
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++) {
double l = euclid(arr[i], arr[j]);
arr2[i][j] = arr2[j][i] = E * l;
}
}
System.out.println();
boolean[] visited = new boolean[N];
double result = 0;
int pickCnt = 0;
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.offer(new Edge(0, 0, 0));
while(!pq.isEmpty()) {
Edge e = pq.poll();
if(visited[e.t]) continue;
visited[e.t] = true;
result += e.w;
if(++pickCnt == N) break;
for(int i = 0; i< N; i++) {
if(!visited[i] && arr2[e.t][i] != 0) {
pq.offer(new Edge(e.t, i, arr2[e.t][i]));
}
}
}
sb.append("#").append(t+1).append(" ").append(Math.round(result)).append("\n");
}
System.out.println(sb);
sc.close();
}
static double euclid(int[] p1, int[] p2) {
return Math.pow(p2[0] - p1[0], 2) + Math.pow(p2[1] - p1[1], 2);
}
static class Edge implements Comparable<Edge> {
int f, t;
double w;
public Edge(int f, int t, double w) {
super();
this.f = f;
this.t = t;
this.w = w;
}
@Override
public int compareTo(Edge o) {
return Double.compare(w, o.w);
}
}
}
알고리즘 QUIZ
- 지하철 게이트를 통과하는 사람들은 Stack이라는 자료구조로 표현하는 것이 적당하다.
- 정답 : X → Queue로 표현
- Queue (FIFO 구조) : 먼저 들어온 사람이 먼저 나감
- Stack (LIFO 구조) : 나중에 들어온 사람이 먼저 나감
- n개의 원소 집합에서 r개를 선택하는 조합의 수를 계산하는 공식은 n!/(r! * (n-r)!) 이다.
- 정답 : O
- 조합은 순서를 고려하지 않는다.
- O(N^2): 입력 크기 N에 비례하여 시간이 증가한다.
- 정답 : X → 입력 크기의 제곱에 비례
- DFS 알고리즘은 스택 자료구조를 사용해 구현 가능하다
- 정답 : O → DFS(깊이 우선)는 재귀적으로 호출될 수 있고, 명시적으로 Stack으로 구현
- BFS 알고리즘은 큐 자료구조를 사용해 구현 가능하다.
- 정답 : O → BFS(너비 우선)는 FIFO 방식으로 탐색하므로 Queue를 사용하여 구현한다.
- ArrayList, Stack, Queue, HashSet은 모두 중복을 허용한다.
- 정답 : X → HashSet은 중복 허용 안함, 나머지는 허용
- Stack에서 요소를 추가하는 메서드는 Enqueue()이다.
- 정답 : X → push()임. Enqueue()는 Queue에서 추가할 때 사용
- Tree , LinkedList, Stack, Queue는 모두 선형 자료구조이다.
- 정답 : X → Tree는 비선형자료구조
- LinkedList는 인덱스를 사용해 임의의 요소에 빠르게 접근할 수 있다.
- 정답 : X → LinkedList는 연속적인 메모리 주소를 사용하지 않으므로, 인덱스로 빠르게 접근할 수 없다.다.
- ArrayList는 O(1) 시간에 인덱스로 접근 가능하지만,
- LinkedList는 처음부터 순차적으로 찾아야 하므로 O(N) 시간이 걸린다.
- 정답 : X → LinkedList는 연속적인 메모리 주소를 사용하지 않으므로, 인덱스로 빠르게 접근할 수 없다.다.
END
This post is licensed under CC BY 4.0 by the author.